from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
# 출처: fgsm tutorial 공식 colab
# NOTE: 아래는 MNIST 데이터셋을 내려받을 때 "User-agent" 관련한 제한을 푸는 코드입니다.
# 더 자세한 내용은 https://github.com/pytorch/vision/issues/3497 을 참고해주세요.
from six.moves import urllib
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)FGSM1 으로 MNIST를 속여보자.
- 입력 데이터에 최소한의 변화를 추가하여 ’잘못 분류되게 하는 것’이 공격자의 목표다.
- 공격의 종류
- 화이트박스: 공격자가 모델의 구조 (입출력, 가중치) 모두를 알고 접근할 수 있다고 가정한다.
- 블랙박스: 공격자가 모델의 입력과 출력단에 접근 가능하고, 모델의 내부는 모른다고 가정한다.
여기서 FGSM은 오분류를 목표로 하는 화이트박스 공격이다.
FGSM
역전파에서 가중치를 조정하여 손실을 ‘최대화’ 하도록 입력 데이터를 조정한다.
구현
- 입력 매개변수를 파악한다.
- 공격할, 공격 중인 모델을 정의한다.
- 공격, 테스트를 진행한다.
입력 매개변수
공격을 받는 모델
MNIST 예제에서 복사해온다. - 모델과 데이터로더 정의 - 모델 초기화 - 학습된 가중치 로드
# LeNet 모델 정의
class Net(nn.Module):
# 네트워크 구조 정의
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# 학습 방법 정의
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)
# MNIST 테스트 데이터셋과 데이터로더 선언
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
])),
batch_size=1, shuffle=True)
# 어떤 디바이스를 사용할지 정의 >> CPU 사용 예정
print("CUDA Available: ",torch.cuda.is_available())
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")
# 모델 초기화하기
model = Net().to(device)
# 미리 학습된 모델 읽어오기
model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))
# 모델을 평가 모드로 설정하기. 드롭아웃 레이어들을 위해 사용됨
model.eval()CUDA Available: FalseNet(
(conv1): Conv2d(1, 10, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(10, 20, kernel_size=(5, 5), stride=(1, 1))
(conv2_drop): Dropout2d(p=0.5, inplace=False)
(fc1): Linear(in_features=320, out_features=50, bias=True)
(fc2): Linear(in_features=50, out_features=10, bias=True)
)FGSM 공격
fgsm_attack함수를 만들어 사용하는데, 이때 입력 파라미터로 위에서 정의한 값들을 넣는다.
- 원본 이미지 \(x\)
- epsilon; pixel 단위의 변화 \(\epsilon\)
- data_grad; 입력 영상에 대한 변화도 손실값
# FGSM 공격 코드
def fgsm_attack(image, epsilon, data_grad):
# data_grad 의 요소별 부호 값을 얻어옵니다
sign_data_grad = data_grad.sign()
# 입력 이미지의 각 픽셀에 sign_data_grad 를 적용해 작은 변화가 적용된 이미지를 생성합니다
perturbed_image = image + epsilon*sign_data_grad
# 값 범위를 [0,1]로 유지하기 위해 자르기(clipping)를 추가합니다
perturbed_image = torch.clamp(perturbed_image, 0, 1)
# 작은 변화가 적용된 이미지를 리턴합니다
return perturbed_image테스트 (*)
테스트 기능을 호출할 때마다 1. 데이터셋에서 전체 테스트 단계를 수행한 후 2. 최종 정확도를 보고한다.
- 여기서도 \(\epsilon\) 을 사용하는데, 테스트 함수가 이에 따라 모델의 정확도를 보고하기 때문이다. (픽셀단위의 변화이므로)
- 공격을 받은 이미지가 작은 변화가 적용된 이미지를 확인한 후 >> 그 이미지의 변화가 적대적인지 확인한다.
def test( model, device, test_loader, epsilon ):
# 정확도 카운터
correct = 0
adv_examples = []
# 테스트 셋의 모든 예제에 대해 루프를 돕니다
for data, target in test_loader:
# 디바이스(CPU or GPU) 에 데이터와 라벨 값을 보냅니다
data, target = data.to(device), target.to(device)
# 텐서의 속성 중 requires_grad 를 설정합니다. 공격에서 중요한 부분입니다 >> 증가시켜야하므로
data.requires_grad = True
# 데이터를 모델에 통과시킵니다
output = model(data)
init_pred = output.max(1, keepdim=True)[1] # 로그 확률의 최대값을 가지는 인덱스를 얻습니다
# 만약 초기 예측이 틀리면, 공격하지 않도록 하고 계속 진행합니다
if init_pred.item() != target.item():
continue
# 손실을 계산합니다
loss = F.nll_loss(output, target)
# 모델의 변화도들을 전부 0으로 설정합니다
model.zero_grad()
# 후방 전달을 통해 모델의 변화도를 계산합니다
loss.backward()
# 변화도 값을 모읍니다
data_grad = data.grad.data
# FGSM 공격을 호출합니다
perturbed_data = fgsm_attack(data, epsilon, data_grad)
# 작은 변화가 적용된 이미지에 대해 재분류합니다
output = model(perturbed_data)
# 올바른지 확인합니다
final_pred = output.max(1, keepdim=True)[1] # 로그 확률의 최대값을 가지는 인덱스를 얻습니다
if final_pred.item() == target.item():
correct += 1
# 0 엡실론 예제에 대해서 저장합니다
if (epsilon == 0) and (len(adv_examples) < 5):
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
else:
# 추후 시각화를 위하 다른 예제들을 저장합니다
if len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
# 해당 엡실론에서의 최종 정확도를 계산합니다
final_acc = correct/float(len(test_loader))
print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
# 정확도와 적대적 예제를 리턴합니다
return final_acc, adv_examples공격 실행
accuracies = []
examples = []
# 각 엡실론에 대해 테스트 함수를 실행합니다
for eps in epsilons:
acc, ex = test(model, device, test_loader, eps)
accuracies.append(acc)
examples.append(ex)Epsilon: 0 Test Accuracy = 9810 / 10000 = 0.981
Epsilon: 0.05 Test Accuracy = 9426 / 10000 = 0.9426
Epsilon: 0.1 Test Accuracy = 8510 / 10000 = 0.851
Epsilon: 0.15 Test Accuracy = 6826 / 10000 = 0.6826
Epsilon: 0.2 Test Accuracy = 4301 / 10000 = 0.4301
Epsilon: 0.25 Test Accuracy = 2082 / 10000 = 0.2082
Epsilon: 0.3 Test Accuracy = 869 / 10000 = 0.0869결과
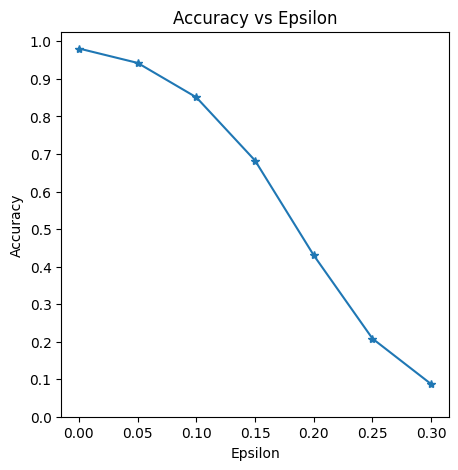
시각화를 진행한다.
엡실론이 증가함에 따라 테스트 정확도가 감소해야 한다.
\(\therefore\) 엡실론 값이 선형적이더라도 곡선의 추세는 선형적이지 않다.
문제
- 엡실론이 증가할수록 정확도는 떨어지지만: 작은 변화는 더 쉽게 인식한다.
- 노이즈가 추가되었더라도 작은 객체는 제대로 선별할 수 있는 경우도 있다.
Footnotes
Fast Gradient Sign Attack↩︎